前言
我们知道循环神经网络(RNN)中一些重要的设计模式包括以下几种:
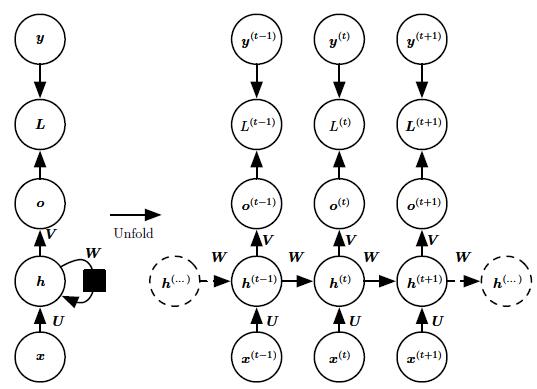
- 每个时间步都有输出,并且隐藏单元之间有循环连接的循环网络,如图 1 所示。
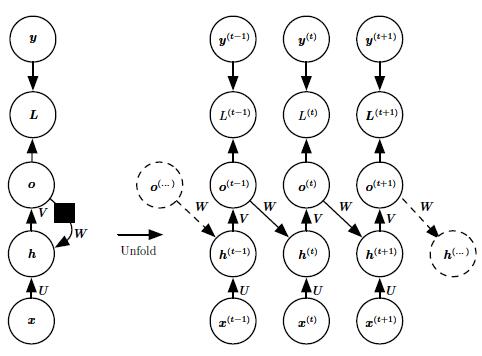
- 每个时间步都产生一个输出,只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络,如图 2 所示。
- 隐藏单元之间存在循环连接,但读取整个序列后产生单个输出的循环网络,如图 3 所示。
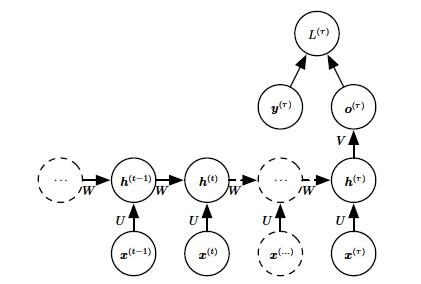
列并产生用于进一步处理的固定大小的表示。在结束处可能存在目标(如此处所示),或者通过更
下游模块的反向传播来获得输出$o(t)$上的梯度。
现在我们研究图 1 中RNN的前向传播公式。这个图没有指定隐藏单元的激活函数。我们假设使用双曲正切激活函数。此外,图中没有明确指定何种形式的输出和损失函数。我们假定输出是离散的,如用于预测词或字符的RNN。表示离散变量的常规方式是把输出$o$作为每个离散变量可能值的非标准化对数概率。然后,我们可以应用$softmax$函数后续处理后,获得标准化后概率的输出向量$ \hat{y}$。RNN 从特定的初始状态$h(0)$开始前向传播。从$t = 1 $到$t = \tau$的每个时间步,我们应用以下更新方程:
$$ \begin{aligned} &a(t) = b + Wh^{(t-1)} + Ux(t); …………..(1) \newline &h(t) = tanh(a(t)); …………..(2)\newline &o(t) = c + Vh(t);…………..(3) \newline &\hat{y}(t) = softmax(o(t)); …………..(4) \end{aligned}$$
其中的参数的偏置向量$b$和$c$连同权重矩阵$U$、$V$ 和$W$,分别对应于输入到隐藏、隐藏到输出和隐藏到隐藏的连接。这个循环网络将一个输入序列映射到相同长度的输出序列。与$x$序列配对的$y$的总损失就是所有时间步的损失之和。
#softmax的导数求解
我们知道softmax函数是用来进行数据归一化的,一般用作结果数据处理,将数据归一化在(0,1)的区间内。其表达式为:
$$S_i =\frac{e^i}{\sum_je^j} $$
对于一个神经网络结构如下图(图片来自网络),其参数计算如下:
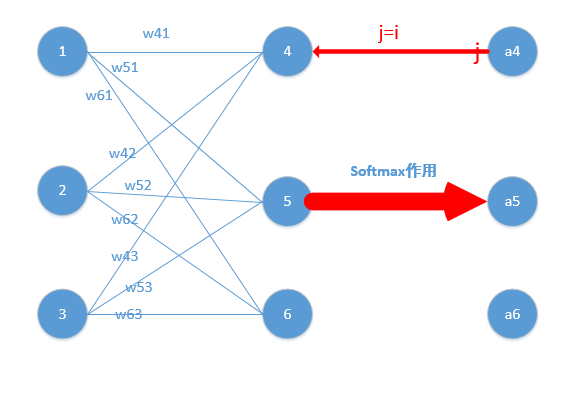
我们可以计算出各个输出函数:
$$z_4 = w_{41}o_1+w_{42}o_2+w_{43}o_3$$
$$z_5 = w_{51}o_1+w_{52}o_2+w_{53}o_3$$
$$z_6 = w_{61}o_1+w{62}o_2+w_{63}*o_3$$
那么我们可以经过softmax函数得到:
$$a_4 = \frac{e^{z_4}}{Z^{z_4}+Z^{z_5}+Z^{z_6}}$$
$$a_5 = \frac{e^{z_5}}{Z^{z_4}+Z^{z_5}+Z^{z_6}}$$
$$a_6= \frac{e^{z_6}}{Z^{z_4}+Z^{z_5}+Z^{z_6}}$$
交叉熵函数形式为:
$$Loss = -\sum_iy_ilna$$
进行求导计算:
如果$i = j$,则
$$ \begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}}) \newline &= \frac{(e^{z_j})^{\prime} \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_j}}{(\sum_k e^{z_k})^2} \newline &=\frac{ e^{z_j} }{\sum_k e^{z_k} } -\frac{ e^{z_j} }{\sum_k e^{z_k} } \cdot \frac{ e^{z_j} }{\sum_k e^{z_k} } \newline &= a_j(1-a_j)\end{aligned} $$
如果$i \ne j$,则
$$ \begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_k e^{z_k}}) \newline &= \frac{ 0 \cdot \sum_k e^{z_k} - e^{z_j} \cdot e^{z_i}}{(\sum_k e^{z_k})^2} \newline &= -\frac{ e^{z_j} }{\sum_k e^{z_k} } \cdot \frac{ e^{z_i} }{\sum_k e^{z_k} } \newline &= -a_ja_i\end{aligned} $$
计算RNN的梯度
计算循环神经网络的梯度是容易的。由反向传播计算得到的梯度,并结合任何通用的基于梯度的技术就可以训练RNN。
为了获得BPTT算法行为的一些直观理解,我们举例说明如何通过BPTT计算上述RNN公式(式(1))的梯度。计算图的节点包括参数$U,V,W,b$和$c$,以及以$t$ 为索引的节点序列$x(t),h(t),o(t)$和$L(t)$。对于每一个节点$N$,我们需要基于$N$后面的节点的梯度,递归地计算梯度$\nabla_NL$。我们从紧接着最终损失的节点开始递归:
$$\frac{\partial L}{\partial L^{(t)}} = 1$$
在这个导数中,我们假设输出$o(t)$作为$softmax$函数的参数,我们可以从$softmax$函数可以获得关于输出概率的向量$\hat{y}$。我们也假设损失是迄今为止给定了输入后的真实目标$y(t)$的负对数似然。对于所有$i,t$,关于时间步$t$输出的梯度$\nabla_{o(t)}L$如下:
$$ (\nabla_{o^{(t)}}L)i = \frac{\partial L}{\partial o{i}^{(t)}} =\frac{\partial L }{\partial L^{(t)}} \frac{\partial L^{(t)} }{\partial o_{i}^{(t)}}= \hat{y}{i}^{(t)} - 1{i,y^{(t)}}$$注:这里将详细的计算推导如下:这个只是个人的逻辑推导,精确推导有待时日再来
$L(t)$ 为给定的$x^{(1)},..,x^{(t)} $后$y(t)$ 的负对数似然:
$$\begin{aligned} L( x^{(1)},..,x^{(t)},y^{(1)},..,y^{(t)}) &= \sum_tL^{(t)}\newline &=-\sum_tlog(p(y^{(t)}|x^{(1)},..,x^{(t)}) \end{aligned}$$
则$L^{(t)}$对$y^{(t)}$求导可以得到一下的结果:
$$\frac{\partial L^{(t)}}{\partial y^{(t)}} \propto -\frac{1}{y^{(t)}}$$
根据之前的softmax函数的推导,我们可以得到 :
$$ \frac{\partial L^{(t)} }{\partial o_{i}^{(t)}} = \frac{\partial L^{(t)}}{\partial y^{(t)}} \frac{ \partial y^{(t)}}{\partial o^{(t)}} = -\frac{1}{y^{(t)}} \cdot y^{(t)}(1-y^{(t)}) = y^{(t)}-1$$
我们从序列的末尾开始,反向进行计算。在最后的时间步$\tau$, $h^{(\tau)}$只有$o^{(\tau)}$ 作为后续节点,因此这个梯度很简单:
$$\nabla_{o^{(t)}}L = V^T \nabla_{o^{(t)}}L$$
然后,我们可以从时刻$t = \tau - 1$到$t = 1$反向迭代,通过时间反向传播梯度,注意$h(t)(t < \tau)$ 同时具有$o(t)$和$h(t+1)$两个后续节点。因此,它的梯度由下式计算这个式子看起来简单但是求解起来很容易出错,因为其中嵌套着激活函数函数,是复合函数的求道过程。
$$ \begin{aligned} \nabla_{h(t)}L &= (\frac{\partial h^{(t+1)}}{\partial h^{(t)}})^T(\nabla_{h(t+1)}L) + (\frac{\partial o^{(t)}}{\partial h^{(t)}})^T(\nabla_{o(t)}L) \newline &=W^T( \nabla_{h(t+1)}L)diag(1-(h^{(t+1)})^2) + V^T(\nabla_{o(t)}L)\end{aligned}$$
其中$diag(1-(h^{(t+1)})^2)$ 表示包含元素 $1-(h_{i}^{(t+1)})^2$的对角矩阵。这是关于时刻$t+1$与隐藏单元i 关联的双曲正切的$Jacobian$。
一旦获得了计算图内部节点的梯度,我们就可以得到关于参数节点的梯度。因为参数在许多时间步共享,我们必须在表示这些变量的微积分操作时谨慎对待。我们希望实现的等式使用$bprop$ 方法计算计算图中单一边对梯度的贡献。然而微积分中的$∇Wf$ 算子,计算$W$ 对于$f$ 的贡献时将计算图中的所有边都考虑进去了。为了消除这种歧义,我们定义只在$t $时刻使用的虚拟变量$W^{(t)}$ 作为W的副本。然后,我们可以使用$∇{W^{(t)}}$ 表示权重在时间步$t $对梯度的贡献。
使用这个表示,关于剩下参数的梯度可以由下式给出:
$$ \begin{aligned} &\nabla_cL = \sum_{t}(\frac{\partial o^{(t)}}{\partial c})^T \nabla_{o^{(t)}}L= \nabla_{o^{(t)}}L, \newline &\nabla_bL = \sum_{t}(\frac{\partial h^{(t)}}{\partial b^{(t)}})^T \nabla_{h^{(t)}}L= \sum_{t}diag(1-(h^{(t)})^2)\nabla_{h(t)}L,\newline &\nabla_VL = \sum_{t}\sum_{i}(\frac{\partial L}{\partial o_{i}^{(t)}})^T \nabla_{V}o^{(t)}= \sum_{t}(\nabla_{o(t)}L)h^{(t)^T}, \newline & \nabla_WL = \sum_{t}\sum_{i}(\frac{\partial L}{\partial h_{i}^{(t)}})^T \nabla_{W^{(t)}}h_{i}^{(t)} = \sum_{t}diag(1-(h^{(t)})^2)(\nabla_{h(t)}L)h^{(t)^T},\newline & \nabla_UL = \sum_{t}\sum_{i}(\frac{\partial L}{\partial h_{i}^{(t)}})^T \nabla_{U^{(t)}}h_{i}^{(t)} = \sum_{t}diag(1-(h^{(t)})^2)(\nabla_{h(t)}L )x^{(t)^T}, \end{aligned}$$
因为计算图中定义的损失的任何参数都不是训练数据$x^{(t)} $的父节点,所以我们不需要计算关于它的梯度。
关于梯度消失和梯度爆炸
在累乘的过程中,如果取$sigmoid$函数作为激活函数的话,那么必然是一堆小数在做乘法,结果就是越乘越小。随着时间序列的不断深入,小数的累乘就会导致梯度越来越小直到接近于0,这就是“梯度消失“现象。其实RNN的时间序列与深层神经网络很像,在较为深层的神经网络中使用$sigmoid$函数做激活函数也会导致反向传播时梯度消失,梯度消失就意味消失那一层的参数再也不更新,那么那一层隐层就变成了单纯的映射层,毫无意义了,所以在深层神经网络中,有时候多加神经元数量可能会比多家深度好。
RNN的特点本来就是能“追根溯源“利用历史数据,现在告诉我可利用的历史数据竟然是有限的,这就令人非常难受,解决“梯度消失“是非常必要的。解决“梯度消失“的方法主要有:
1、选取更好的激活函数
2、改变传播结构
关于第一点,一般选用$ReLU$函数作为激活函数,
ReLU函数的左侧导数为0,右侧导数恒为1,这就避免了“梯度消失“的发生。但恒为1的导数容易导致“梯度爆炸“,但设定合适的阈值可以解决这个问题。还有一点就是如果左侧横为0的导数有可能导致把神经元学死,不过设置合适的步长(学习旅)也可以有效避免这个问题的发生。
$sigmoid$函数还有一个缺点,$Sigmoid$函数输出不是零中心对称。$sigmoid$的输出均大于0,这就使得输出不是0均值,称为偏移现象,这将导致后一层的神经元将上一层输出的非0均值的信号作为输入。关于原点对称的输入和中心对称的输出,网络会收敛地更好。